Luis Puente

The handle was designed to support the force applied by the user, the force to fracture the mandrel, a spring force, and finally a reaction force. The handle part is shown below along with its free body diagram (Figure 1 & Figure 2).

Shear and moment diagrams were calculated to find the maximum forces in the handle. The shear diagram was calculated using the method of sections while the moment diagram was calculated by integrating the shear diagram. Both diagrams are shown below (Figure 3).

When considering the bending stress in the handle, the maximum magnitude occurs at 9.538 inches away from the end of the handle as seen in the moment diagram (Figure 3). This maximum moment is located at the location of the first hole where the pivot pin is inserted. Since the handle supports the pin load between two extruded walls, the max moment is divided by two. The bending moment is zero at the neutral axis and maximum at the furthest radial distance of the handle, so we analyzed point 1 (marked in Figure 4 below). We can then calculate the maximum nominal stress in each of the two parts of the handle supporting the load by considering a rod without any holes.

To account for the stress concentrations of the holes, we used the charts of theoretical stress-concentration factors Kt. Being that we are considering a bending moment, we used Figure A-15-2 from Shigley’s Mechanical Design textbook [1].

Next, we calculated the transverse shear stress on each of the two extruded members of the handle by considering the maximum shear force from the shear diagram (Figure 3). The maximum shear stress on the members with the hole occurs at the centerline of each extruded piece. This point is marked by point 2 in Figure 4. We considered the stress at this point with the cross-sectional area of each extruded piece to account for the shared load of each member and the hole.

As seen above, the handle would fail first due to bending stress since it is almost three times larger than the shear stress on each member with a hole. Thus, we continue to analyze the principal stresses and safety factor based on the maximum bending stress calculated above (𝜎𝑚𝑎𝑥).

As seen from the von Mises stress calculations above, the handle can be considered safe since its safety factor is greater than n=1. We then examine fatigue on the handle due to variable loading from use. To do this we calculate the modified endurance limit.

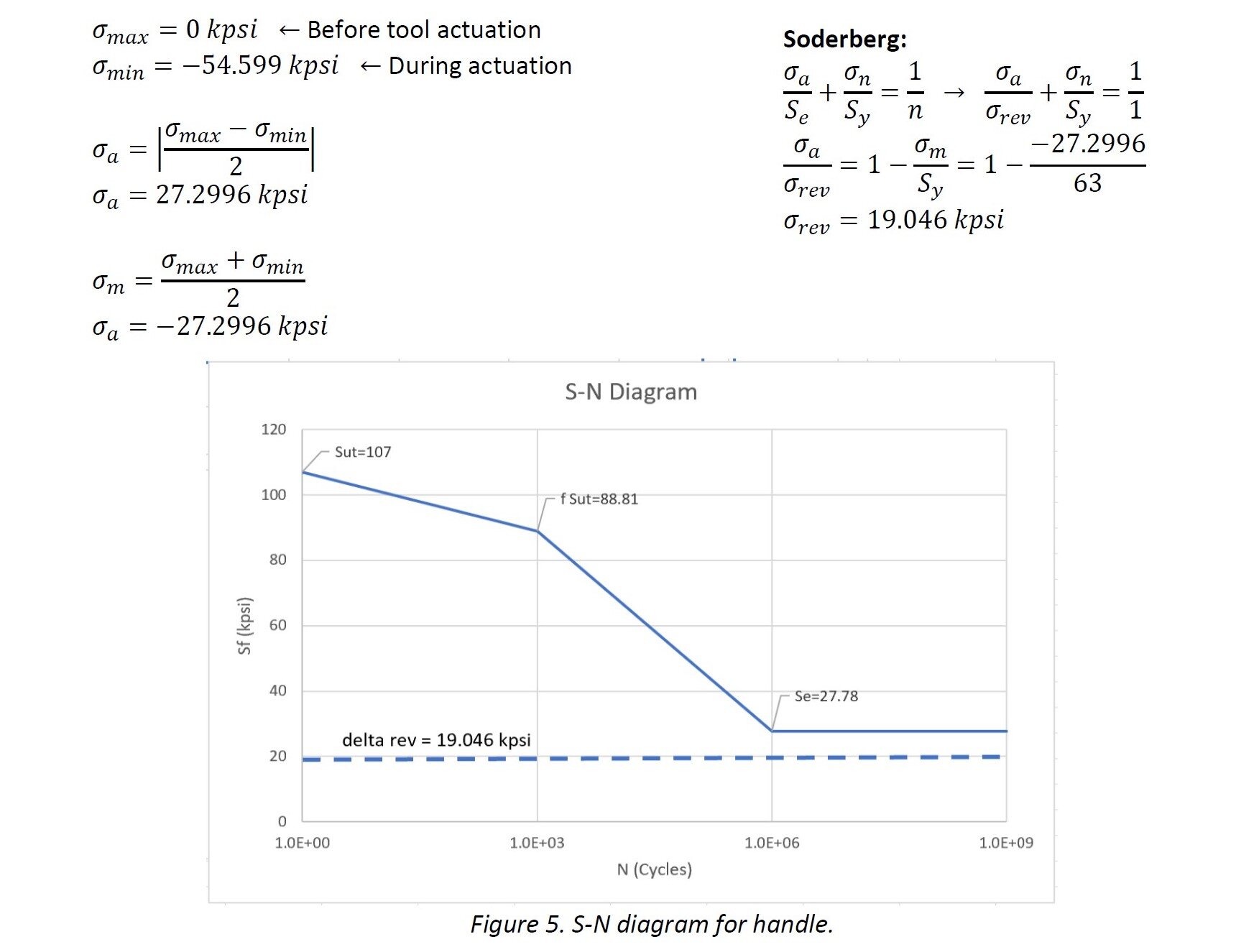
To estimate the number of cycles to failure for the handle we then obtain the fully-reversed stress 𝜎𝑟𝑒𝑣 and compare it to the modified endurance limit calculated above. To calculate the fully-reversed stress we used the Soderberg approximation since this is the most conservative approach.

As seen from the S-N diagram above (Figure 5), the fully-reversed stress 𝜎𝑟𝑒𝑣 is below the endurance limit. Due to this inequality, we can conclude that the handle will have an infinite life based on the Soderberg criteria.