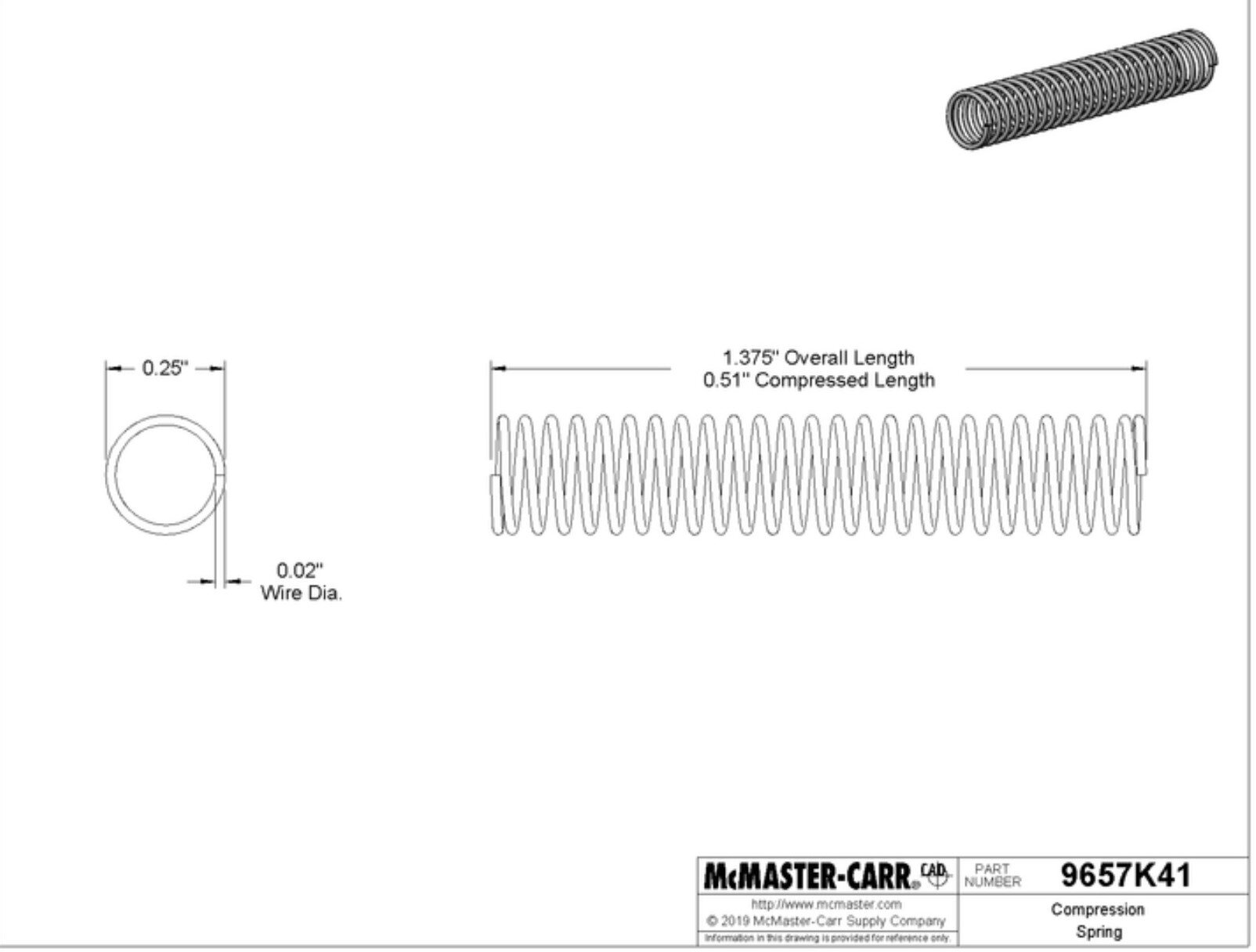
Spring
The spring was by taking different wire diameter iterations. While setting a range of wire diameters we will use the preferred end, squared and grounded. Throughout this process several values will be calculated. This will help find a spring for the rivet gun (Table). These measurements will be in mind with the 4lb load. The material properties we will be using ASTM A228 Steel (UNS K08500), cold drawn music wire. This will have the shear modulus of the material.
From this information we can now find the (k) value with is lbs./in that will can solved using algebra through the equation of Dcoil of the spring. Now we use the 4lb load to find max keep in mind this will not be the same from the table. This is another form of calculating stress values. Since this is a compression spring; through a diagram we see what is affect the cross-section is torsion and shear. Where the shear is equal to the force applied and the torque is equal to the force time the diameter by half.
From here we see that shear and torsion are going in the same direction. Since shear is max at the center and torsion is max at the edge. After finding the stress we can now find the principle stress of this cross-sectional area.
After finding the principle stress we can go ahead and Von Misses
This will then be followed by the fatigue of the spring. Since we are using the Soderberg criterion since it is the most conservative.
Through the table it shows the Sut value of the spring and use it to calculate the values for a S-N diagram. Since the value of Sut the fraction of f can be found on the experimental data sheet.
This shows through Soderberg criteria is shows the σrev is less than Se showing that it may last to infinity.
Chosen Spring